当前位置:主页 > MBA科目 > >>数学专题系列丨不定方程在应用题中的应用
数学专题系列丨不定方程在应用题中的应用
- 作者:莘洲教育
- 时间:2018-12-29 15:06
- 点击数:
不定方程定义:未知数的个数多于方程个数,是未知数受到某些限制(如有理数,整数等等)的方程或方程组
解题技巧:利用奇偶性、利用特殊倍数关系、利用极限值
典型题型如下:
1.(2017真题)某公司用1万元购买了价格分别是1750元和950元的甲、乙两种办公设备,则购买的
甲、乙办公设备的件数分别为( ).
A. 3,5 B. 5,3 C. 4,4 D. 2,6 E .6,2
2.(2015真题)在某次考试中,甲、乙、丙三个班的平均成绩为80, 81和81. 5,三个班的学生得分之
和为6952,三个班共有学生( )名.
A. 85 B. 86 C. 87 D. 88 E. 90
3.(2013真题)某单位年终共发了100万元奖金,奖金金额分别是一等奖1.5万元,二等奖1万元,三等奖0.5万元,则该单位至少有100人.
(1)得二等奖的人数最多. (2)得三等奖的人数最多.
4.(2011真题)在年底的献爱心活动中,某单位共有100人参加捐款,据统计,捐款总额是19000元,个人捐款数额有100元、500元和2000元三种,该单位捐款500元的人数为( ).
A. 13 B. 18 C. 25 D. 30 E. 38
答案解析
1、A
考点:实数、简单方程
分析:设购买甲、乙办公设备的件数分别为a,b.
则1750a+950b=10000,化简有35a+19b=200.
代入选项验证,可得a=3,b=5(也可观察,35a必为5或者0结尾,则b必须为5或者10的倍数才能保障右边为200,故答案选A)
2、B
分析:利用思维解题法,人数应该处于6952/81.5和6952/80之间,可以得出只有整数86符合条件.
3、B
分析:利用思维解题法
设获得一等奖1.5万元,二等奖1万元,三等奖0.5万元的人数分别是x,y,z.
由题意得到1.5x+y+0.5z=100得到x+y+z=100+0.5(z-x),
明显与y无关,只需要z>x即可,因此有条件(1)不充分,条件(2)充分.
4、A
分析:利用偶数法、尾数法
捐款100元、500元、2000元的人数分别为x, y, z,
由题意得到
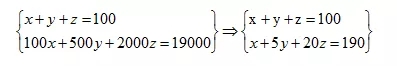
易得到4y+19z=90,
根据偶数+偶数=偶数的性质得到z一定为偶数,
可令z=2代人验证,得到y=13,只有唯一正确解,因此就为13人.
上一篇:没有了 下一篇:数学不等式与线性规划应用题
相关文章:











 无锡专硕考研
无锡专硕考研 莘洲教育微博
莘洲教育微博